Теплота политропного процесса определяется по одному из следующих выражений
Обновлено: 29.10.2024
Политропный процесс характеризуется тем, что он протекает в идеальном газе при постоянном значении теплоемкости, которая может иметь любое числовое значение от – ∞ до + ∞.
Для политропного процесса доля количества теплоты, расходуемой на изменение внутренней энергии, остается неизменной:
Выведем уравнение политропы. Пусть сn – теплоемкость политропного процесса. В соответствии с уравнениями (dL = pdV, dq = du + dL, dqv = du = сvdT) получим:
Используя уравнение (dh = du + pdv + vdp = dq + vdp), после ряда преобразований будем иметь:
Так как из определения политропного процесса следует, что теплоемкость – величина постоянная, то обозначив
после интегрирования получим:
Это уравнение называется уравнением политропного процесса, а n – показателем политропы.
Для политропы справедлива следующая связь между основными параметрами состояния:
Работу политропного процесса можно определить по формулам:
Для определения работы М кг газа нужно в приведенных формулах заменить удельный объем v полным объемом газа V.
Теплоемкость политропного процесса можно найти из уравнения:
Количество теплоты, сообщаемой газу или отнимаемой от него:
Изменение внутренней энергии газа в политропном процессе находим по общей для всех процессов формуле:
Показатель политропного процесса определяется из уравнения:
Изменение энтропии:
Политропный процесс включает в себя всю совокупность основных термодинамических процессов и поэтому имеет и обобщающее значение. На самом деле из уравнений и нетрудно прийти к выводу, что:
при n = ± ∞ сn = сv и v = const (изохорный процесс);
при n = 0 сn = сp и р = const (изобарный процесс);
при n = 1 сn = ∞ и рv = const (изотермный процесс);
при n = k сn = 0 и pv k = const (адиабатный процесс).
На рисунке 4.5 в pv – и Ts – координатах приведены совмещенные графические зависимости различных термодинамических процессов.
Все процессы можно разделить на три группы (рисунок 4.5).
Группа I (– ∞ < n < 1). Графики процессов этой группы располагаются между изохорой и изотермой. Расширение осуществляется с подводом теплоты, которая идет на увеличение внутренней энергии и на совершение работы. С увеличением n доля теплоты, идущей на увеличение внутренней энергии, уменьшается, а доля теплоты, идущей на совершение работы, растет; соответственно будет расти доля теплоты, идущей на совершение работы от 0 при n = –∞ до 1 при n =1. Теплоемкость положительна.
Группа II (1 < n < k). Графики процессов располагаются между изотермой и адиабатой. Работа получается за счет подводимой теплоты и уменьшения внутренней энергии. Доля теплоты, идущей на изменение внутренней энергии, отрицательна, так как q и Δu имеют разные знаки. По мере увеличения показателя n все большая часть работы получается за счет внутренней энергии и все меньшая – за счет подвода теплоты к рабочему телу. Соответственно доля внутренней энергии, расходуемой на совершение работы, возрастает с 1 до ∞, а доля теплоты, расходуемой на совершение работы, уменьшается с ∞ до –1.
Теплоемкость отрицательна. Это хорошо видно из формулы . Так как сn= dq/dT, то отрицательная сn означает, что dq и dT имеют противоположные знаки. Несмотря на подвод к газу теплоты, его температура падает, и наоборот. В таких процессах l > q, поскольку на совершение работы помимо подводимой теплоты расходуется часть внутренней энергии газа и его температура понижается.
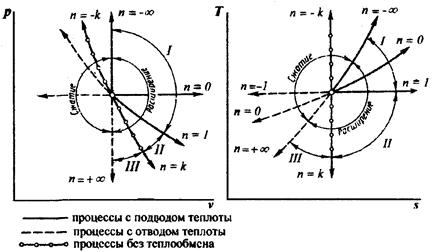
Рис. 4.5 – Политропные процессы в pv и Тs – координатах
Группа III (+ ∞ > n > k). Графики этих процессов располагаются между адиабатой и изохорой. При расширении газа процесс осуществляется с уменьшением внутренней энергии, с совершением работы и отводом тепла в холодильник. С увеличением показателя n увеличивается доля теплоты, отводимой в холодильник, и уменьшается доля теплоты, идущей на совершение работы. Теплоемкость положительна. Доля теплоты, расходуемой на совершение работы, уменьшается с ∞ до 0, а доля внутренней энергии, расходуемой на совершение работы, с –1до 0.
Читайте также:

